CBSE Sample Paper for Class 10th Mathematics Paper 05 | CBSE Notes

Here we are giving sample paper to all of you CBSE board students, through which all of you can score very well in your exams. In this post, we are giving you a sample paper of class 10 maths. hope you benefit from it. You can download the pdf file of this sample paper. CBSE sample paper 2021 class 10 and CBSE sample paper 2021 class 12

CBSE Sample Paper for Class 10th Mathematics Paper 05 | CBSE Exam

Board	CBSE
Class	X ( 10th )
Subject	Mathematics
Sample Paper No.	Paper 05
Category	CBSE Sample Paper

Students who are going to appear for CBSE Class 10 Examinations are advised to practice the CBSE sample papers given here which is designed as per the latest Syllabus and marking scheme, as prescribed by the CBSE, is given here. Paper 1 of Solved CBSE Sample Paper for Class 10 Maths is given below with free pdf download solutions.

Time allowed: 3 Hours
Maximum Marks: 80

General Instructions

• All questions are compulsory.
• The question paper consists of 30 questions divided into four sections A, B, C, and D.
• Section A contains 6 questions of 1 mark each. Section B contains 6 questions of 2 marks each. Section C contains 10 questions of 3 marks each. Section D contains 8 questions of 4 marks each,
• There is no overall choice. However, an internal choice has been provided in four questions of 3 marks each and three questions of 4 marks each. You have to attempt only one of the alternatives in all such questions.
• Use of calculators is not permitted.

Section-A

Question 1.
Can the number 6n, n being number, end with the digit 5? Give reasons.

Question 2.
ABC is an isosceles triangle in which AB = AC = 10 cm. BC = 12 cm. PQRS is a rectangle inside the
isosceles triangle. Given PQ = SR = 2x cm and PS = QR = y cm. Prove that xb = 6 – [latex s=2]\frac { 3y }{ 4 } [/latex]

Question 3.
Find the middle term oftheA.P. 6,13,20,……..,216.

Question 4.
Represent in the form of quadratic equation : (x – 3) (2x + 1) = x (x + 5).

Question 5.
Find the third vertex of a triangle, if two of its vertices are at (-3, 1) and (0,-2) and the centroid is at the origin.

Question 6.
Prove: [latex s=2]\frac { \sin ^{ 4 }{ \theta } -\cos ^{ 4 }{ \theta } }{ \sin ^{ 2 }{ \theta } -\cos ^{ 2 }{ \theta } } [/latex] = 1

Section-B

Question 7.
Use Euclid’s algorithm to find the HCF of 6812 and 289 f6.

Question 8.
Find the relation between x and y if the points A(x, y), B (-5,7), and C (-4,5) are collinear.

Question 9.
From a normal pack of cards, a card is drawn at random, find the probability of getting a jack or a king.

Question 10.
Find the value of K for which the system of equations has no solution.
3x +y = 1; (2k – 1)x + (k – 1)y = (2k + 1)

Question 11.
Which term of the progression 20, 19 [latex s=2]\frac { 1 }{ 4 } [/latex],18[latex s=2]\frac { 1 }{ 2 } [/latex],17 [latex s=2]\frac { 3 }{ 4 } [/latex],…… is the first negative term?

Question 12.
In a single throw of two dice, find the probability of getting a sum of 10.

Section-C

Question 13.
Prove that if x and y are odd positive integers, then x2 + y2 is even but not divisible by 4.

Question 14.
If a, B are the roots of the polynomials^) = 2x2 + 5x + k satisfying the relation α2 + β2 + αβ = [latex s=2]\frac { 21 }{ 4 } [/latex], then find the value of k for this to be possible.

Question 15.
In the figure, ABC is a right triangle, right-angled at B. AD and CE are two medians drawn from A and C
respectively. If AC= 5 cm and AD = [latex s=2]\frac { 3\sqrt { 5 } }{ 2 } [/latex] cm, find the length of CE.

OR
In ∆ABC, AD⊥BC and point D lies on BC such that 2DB = 3CD. Prove that 5AB2 = 5AC2 + BC2

Question 16.
Solve the following equations: [latex s=2]\frac { 1 }{ 7x } +\frac { 1 }{ 6y } [/latex] = 3, [latex s=2]\frac { 1 }{ 2x } -\frac { 1 }{ 3y } [/latex] = 5

Question 17.
If cos θ +[latex]\sqrt { 3 } [/latex] sinθ = 2sinθ . Show that sin θ – [latex]\sqrt { 3 } [/latex]cos θ = 2cos θ.
OR

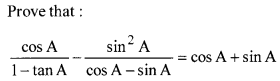
Question 18.
If A (-1,-1), B (-1,4), C (5,4) andD (5,-1) are the vertices of a quadrilateral ABCD, find its area.
OR
ABCD is a rectangle formed by the points A(-l, -1), B(- 1,4), C(5, 4) and D(5, – 1). P, Q, R, and S are the mid-points of AB, BC, CD, and DA, respectively. Is the quadrilateral PQRS a square? a rectangle? or a rhombus? Justify your answer.

Question 19.
A boy is cycling such that the wheels of the cycle are making 140 revolutions per minute. If the diameter of the wheel is 60 cm, calculate the speed per hour with which the boy is cycling.

Question 20.
The numbers 5, 7, 10, 12, 2x-8, 2x+ 10, 35, 41, 42, 50 are arranged in ascending order. If their median is 25 then find the value of x.

Question 21.
Prove that the line segment joining the points of contact of two parallel tangents of a circle passes through its center.

Question 22.
A well of diameter 4 m is dug 14 m deep. The earth taken out is spread evenly all around the well to form a 40 cm high embankment. Find the width of the embankment.
OR
A sphere of diameter 12.6 cm is melted and recast into a right circular cone of a height of 25.2 cm. Find the diameter of the base of the cone.

Section-D

Question 23.
Prove that (sin A + cosec A)2 + (cos A + sec A)2 = 7 + tan2 A + cot2 A.

Question 24.
In an AP of 50 terms, the sum of the first 10 terms is 210 and the sum of its last 15 terms is 2565. Find the A.P.

Question 25.
Solve the equation by using qudratic formula : (x + 4) (x + 5) = 3(x + 1) (x + 2) + 2x
OR
If the roots of the equation (c2 – ab) x2 – 2(a2 – bc) x + (b2 – ac) = 0 are equal, prove that either a = 0 or a3 + b3 + c3 = 3abc

Question 26.
If the areas of two similar triangles are equal, prove that they are congruent.
OR
Sides AB and BC and median AD of a triangle ABC are respectively proportional to sides PQ and QR and median PM of triangle PQR. Prove that ∆ABC ~ ∆PQR

Question 27.
The angle of elevation of the top of a tower at a distance of 120 m from a point A on the ground is 45°. If the angle of elevation of the top of a flagstaff fixed at the top of the tower, at A is 60°, then find the height
of the flagstaff. [Use [latex]\sqrt { 3 } [/latex] = 1.73]
OR
From a point P on the ground, the angle of elevation of the top of a tower is 30° and that of the top of a flagstaff fixed on the top of the tower, is 60°. If the length of the flagstaff is 5m, find the height of the tower.

Question 28.
The mean of three positive numbers is 10 more than the smallest of the numbers and 15 less than the largest of the three. If the median of the three numbers is 5, then find the means of squares of the numbers. (NTSE 2016)

Question 29.
Draw a right triangle ABC in which AB = 6 cm, BC = 8 cm and ∠B = 90°. Draw BD perpendicular from B on AC and draw a circle passing through the points B, C and D. Construct tangents from A to this circle.

Question 30.
The diameter of the internal and external surfaces of a hollow spherical shell are 6 cm and 10 cm, respectively.
Ifit is melted and recast into a solid cylinder of length 2[latex s=2]\frac { 3 }{ 2 } [/latex] cm. Find the diameter ofthe cylinder.

Solutions
Section-A

Solution 1.
If 6n ends with 5, then it must have 5 as a factor. Prime factors of 6n are 2 and 3.
∴ 6n = (2 × 3)n = 2n × 3n
The fundamental theorem of arithmetic, the prime factorization of every composite number is unique.
∴ 6n can never end with 5. (1)

Solution 2.

Solution 3.
The given A.P. is 6, 13, 20, ………..,216
Here, d = 7, a = 6
an = a + (n-1)d
∴216 = 6 + (n- 1) × 7 ⇒n = 31

∴a16= 6+ 15 × 7 = 111 (1)

Solution 4.
(x-3)(2x+l)-x(x + 5)
2x2 – 5x – 3 = x2 + 5x
x2 – 10x – 3 = 0 (1)

Solution 5.
Let th e third vertex of the triangle PQR be given by P (x, y).
By definition of centroid of a triangle, we have [latex s=2]\frac { -3+0+x }{ 3 } [/latex] = 0 [∵The centroid is at the origin]
and [latex s=2]\frac { 1-2+y }{ 3 } [/latex] = 0
From above : x = 3 and y = 1

∴ The required third vertex is (3,1)

Solution 6.
Expressing sin4θ -cos4θ as (sin2θ)2 – (cos2θ)2
⇒ sin4 θ -cos4 θ
= (sin2θ -cos2θ). (sin2θ + cos2θ)
Now, we know that sin2θ + cos2θ = 1
∴ [latex s=2]\frac { \sin ^{ 4 }{ \theta } -\cos ^{ 4 }{ \theta } }{ \sin ^{ 2 }{ \theta } -\cos ^{ 2 }{ \theta } } [/latex] = 1 = R.H.S. (Hence Proved) (1)

Section-B

Solution 7.
Since, 28916 > 6812, we apply division lemma to 28916 and 6812, to get
28916 = 6812 × 4+1668
6812=1668 × 4+140 (1/2)
1668= 140 × 11 + 128
140= 128 × 1 + 12 (1/2)
128= 12 × 10 + 8
12= 8 × 1 +4 (1/2)
8 =4 × 2 + 0
The remainder has become zero. Now our procedure stops. At this stage, the divisor is 4. So the HCF(6812,28916) is 4. (1/2)

Solution 8.
By ar (∆ABC) = 0 for collinear points A, B and C.
∴x(7 – 5)-5(5 – y)-4(y – 7) = 0 (1)
So, 2x – 25 +5y – 4y + 28 = 0 (1/2)
Hence, 2x + y + 3 = 0 (1/2)

Solution 9.
n(S) = 52, n(E) = 4 + 4 = 8 (1)
P(E) = [latex s=2]\frac { n(E) }{ n(S) } [/latex] = [latex s=2]\frac { 8 }{ 52 } [/latex] = [latex s=2]\frac { 2 }{ 13 } [/latex] (1)

Solution 10.

Solution 11.

Solution 12.
n(S) = 6x 6= 36, E = {(4,6), (5,5), (6,4)} n(E) = 3
n(E) = 3 (1)
P(E) = [latex s=2]\frac { n(E) }{ n(S) } [/latex] = [latex s=2]\frac { 3}{ 36 } [/latex] = [latex s=2]\frac { 1 }{ 12 } [/latex] (1)

Section-C

Solution 13.
We know that any odd positive integer is of the form 2q + 1 for some whole number q.
So, let x = 2m + 1 and y = 2n + 1 for some whole number m and n.

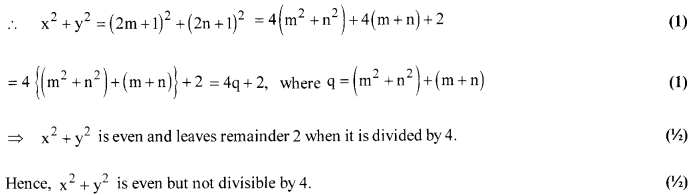
Solution 14.

Solution 15.

OR

Solution 16.

Solution 17.

OR

Solution 18.

OR

Solution 19.

Solution 20.
N= 10 (even).
Median = [latex s=2]\frac { 1 }{ 2 } [/latex] (5th obs. + th obs.) (1)
= [latex s=2]\frac { 1 }{ 2 } [/latex] (2x – 8 + 2x+ 10) =2x+1 (1)
2x+1=25 ⇒ x=12. (1)

Solution 21.
Given : Tangents AB and DC are parallel
To Prove : PQ passing through centre O
Const: DrawEO || AB

Proof :AB || DC
The Sum of the angles on the same side of the transversal is 180°
∠APO + ∠EOP=180° ⇒ ∠EOP= 180°-90° =90° (1)
Similarly, ∠EOQ = 90°
∴ ∠EOP + ∠EOQ = 90° + 90° = 180°
∴ PQ is a straight line
Elance PQ passing through the center O. (1)

Solution 22.

Section-D

Solution 23.
L.H.S. = (sinA + cosec A)2 + (cos A + sec A)2
= sin2 A + cosec2 A + 2 + cos2 A + sec2 A + 2 (2)
= 5 + 1 + cot2 A + 1 + tan2 A (1)
= 7 + cot2 A + tan2 A = R.H.S. (1)

Solution 24.

Solution 25.

OR

Solution 26.

OR

Solution 27.

OR

Solution 28.

Solution 29.

Steps:
(i) Draw AABC and perpendicular BD on AC
(ii) Draw a circle with BC as diameter.
(iii) Circle passing through B, C, and D.
(iv) Let Q be the midpoint of BC. Join AQ.
(v) Draw a circle with AQ as diameter. This circle cuts the previous circle at points P and B.
(vi) Now, join AP and AB are desired tangents drawn from A to the circle passing through B, C
, and D. (1)

Solution 30.

 

 

Download PDF file  Click Here!!!

 

I hope you like the information and notes given by us. This will help you a lot in your upcoming exams. Here we are giving sample papers to all of you CBSE board students, through which all of you can score very well in your exams. In this post, we are giving you a sample paper of class 10 maths. hope you benefit from it. You can download the pdf file of this sample paper.