Here we are giving sample papers to all of you CBSE board students, through which all of you can score very well in your exams. In this post, we are giving you a sample paper of class 10 maths. hope you benefit from it. You can download the pdf file of this sample paper. cbse sample paper 2021 class 10 and cbse sample paper 2021 class 12
CBSE Sample Paper for Class 10th Mathematics Paper 04 | CBSE Exam
| Board | CBSE |
| Class | X ( 10th ) |
| Subject | Mathematics |
| Sample Paper No. | Paper 04 |
| Category | CBSE Sample Paper |
Students who are going to appear for CBSE Class 10 Examinations are advised to practice the CBSE sample papers given here which is designed as per the latest Syllabus and marking scheme, as prescribed by the CBSE, is given here. Paper 1 of Solved CBSE Sample Paper for Class 10 Maths is given below with free pdf download solutions. cbse sample paper 2021 class 10 and cbse sample paper 2021 class 12
Time allowed: 3 Hours
Maximum Marks: 80
General Instructions
- All questions are compulsory.
- The question paper consists of 30 questions divided into four sections A, B, C and D.
- Section A contains 6 questions of 1 mark each. Section B contains 6 questions of 2 marks each. Section C contains 10 questions of 3 marks each. Section D contains 8 questions of 4 marks each,
- There is no overall choice. However, an internal choice has been provided in four questions of 3 marks each and three questions of 4 marks each. You have to attempt only one of the alternatives in all such questions.
- Use of calculators is not permitted.
Section-A
Question 1.
The values of the remainder r, when a positive integer a is divided by 3 are 0 and 1 only. Justify your answer.
Question 2.
Find the altitude of an equilateral triangle when each of its side is ‘a’ cm.
Question 3.
If x =[latex s=2]\frac { 2 }{ 3 } [/latex] and x = – 3 are roots of the quadratic equation ax2 + 7x + b = 0, find the values of a and b.
Question 4.
If A + B = 90° and sec A =[latex s=2]\frac { 5 }{ 3 } [/latex] , then find the value of cosec B.
Question 5.
The first three terms of an AP respectively are 3y – 1, 3y + 5, and 5y + 1. Then find y.
Question 6.
Find the value of x such that PQ = QR where coordinates of P, Q, R are (6, -1), (1, 3), and (x, 8) respectively.
Section-B
Question 7.
Find the LCM of 66 & 486 by the Prime factorization method. Hence find their HCF.
Question 8.
The sum of the 5th and the 9th terms of an AP is 30. If its 25th term is three times its 8th term, find the AP.
Question 9.
A bag contains 5 red balls and some blue balls. If the probability of drawing a blue ball is double that of a red ball, then find the number of blue balls in the bag.
Question 10.
Find the area of the triangle ABC with A (1, – 4) and mid-points of sides through A being (2, -1) and (0,-1).
Question 11.
Find the value of a so that the point (3, a) lies on the line represented by 2x – 3y = 5.
Question 12.
Two dice are thrown simultaneously. What is the probability that the sum of the numbers appearing on the dice is a prime number?
Section-C
Question 13.
Find the HCF of 81 and 237 and express it as a linear combination of 81 and 237.
Question 14.
If a and (1 are the zeroes of the quadratic polynomial p(s) = 3 s2 – 6s + 4, find the value of
[latex s=2]\frac { \alpha }{ \beta } +\frac { \beta }{ \alpha } +2\left( \frac { 1 }{ \alpha } +\frac { 1 }{ \beta } \right) +3\alpha \beta [/latex].
Question 15.
In fig., PSR, RTQ, and PAQ are three semicircles of diameters 10 cm, 3 cm, and 7 cm respectively. Find the perimeter of the shaded region.
[Use π = 3.14]

Question 16.
150 spherical marbles, each of diameter 1.4 cm, are dropped in a cylindrical vessel of diameter 7 cm containing some water, which is completely immersed in water. Find the rise in the level of water in the vessel.
OR
The volume and surface area of a solid hemisphere are numerically equal. What is the diameter of the hemisphere?
Question 17.
The three vertices of a parallelogram ABCD are A(3,^l), B(-l,-3), and C(-6,2). Find the coordinates of vertex D and find the area of ABCD.
Question 18.
If sec θ + tan θ = p, then prove that [latex s=2]\frac { { p }^{ 2 }-1 }{ { p }^{ 2 }+1 } [/latex] = sin θ
OR
If α + β = 90° and α = 2β , then find the value of cos2 α + sin2 β
Question 19.
If the median for the following frequency distribution is 28.5, find the values of X and y:

OR
The mean of marks scored by 100 students was found to be 40. Later on, it was discovered that a score of 53 was misread as 83. Find the correct mean.
Question 20.
In the adjoining figure, PA and PB are tangents to a circle with centre O. If OP is equal to the diameter of the circle, prove that ∆ABP is an equilateral triangle.

Question 21.
Solve: 2x2 +3y2 = 35; [latex s=2]\frac { { x }^{ 2 } }{ 2 } +\frac { { y }^{ 2 } }{ 3 } [/latex] = 5
Question 22.
Sides AB and BC and median AD of a triangle ABC are respectively proportional to sides PQ and QR and median PM of triangle PQR. Prove that ∆ABC ~ ∆PQR
OR
In the given figure, ∆ABC and ∆DBC are on the same base BC. AD and BC intersect at O. Prove that
[latex]\frac { ar(\triangle ABC) }{ ar(\triangle DBC) } =\frac { AO }{ DO } [/latex].

Section-D
Question 23.
On a straight line passing through the foot of a tower, two points C and D are at distances of 4 m and 16m from the foot respectively. If the angles of elevation from C and D of the top of the tower are complementary, then find the height of the tower.
OR
The angles of elevation and depression of the top and the bottom of a tower from the top of a building, 60 m high, are 30° and 60° respectively. Find the difference between the heights of the building and the tower and the distance between them.
Question 24.
An iron pole consisting of a cylindrical portion 110 cm. high and of base diameter 12cm. is surmounted by a cone 9 cm. high. Find the mass of the pole, given that 1 cm3 of iron has 8 gram mass (approx.).
[use 71 = 355/113].
Question 25.
If one angle of a triangle is equal to one angle of the other triangle and the sides including these angles are proportional, then prove that the two triangles are similar.
OR
If a line divides any two sides of a triangle in the same ratio, then prove that the line is parallel to the third side.
Question 26.

Question 27.
Draw a circle of radius 4 cm. Take a point P outside the circle. Without using the centre of the circle, draw two tangents to the circle from point P.
Question 28.
The frequency distribution of scores obtained by 230 candidates in a medical entrance test is as follows:

Draw cumulative frequency curve or ogive by more than method.
Question 29.
If the equation (1 + m2) x2 + 2mcx + c2 – a2 = 0 has coincident roots show that c2 = a2 (1 + m2)
or c = ±a[latex]\sqrt { 1+{ m }^{ 2 } } [/latex] .
OR
If x = 4 and x = -5 are roots of3x2-2mx + 2n = 0, find the values of ‘m’ and ‘n’.
Question 30.
If four numbers in A.P. are such that their sum is 50 and the greatest number is 4 times the least, then find the numbers.
Solutions
Section-A
Solution 1.
No. According to Euclid’s division lemma, a=3q + r, where 0 ≤ r < 3 and r is an integer. Therefore, the values of r can be 0, 1 or 2. (1)
Solution 2.

Solution 3.

Solution 4.
Given, A + B = 90° and sec A = [latex s=2]\frac { 5 }{ 3} [/latex]
⇒ sec(90°-B) =[latex s=2]\frac { 5 }{ 3} [/latex] (∵ A + B = 90°)
∴ cosec B = [latex s=2]\frac { 5 }{ 3} [/latex] (1)
Solution 5.
a1 = 3y- 1, a2 = 3y+ 5, a3 = 5y+ 1
∴ a2 – a1 = 3 – a1
⇒(3y + 5) – (3y- 1) = (5y + 1) – (3y +5) ⇒6 = 2y-4 (1)
⇒ 2y=10 ⇒ y=5
Solution 6.
Since, PQ = QR ⇒ Q is mid-point of PR.
∴ Using mid-point formula,
1 = [latex s=2]\frac { 6+x }{ 2} [/latex] ⇒ 6 + x = 2 ⇒x = -4. (1)
Section-B
Solution 7.
The Prime factorisation of 66 & 486 gives
66 = 2 × 3 × 11
486 = 2 × 3 ×3 ×3 × 3 × 3= 2 × 35 (1/2)
∴The LCM of these two integer is
2 × 35 × 11 = 5346 (1/2)
HCF (66,486) = [latex]\frac { 66\times 486 }{ LCM(66,486) } =\frac { 66\times 486 }{ 5346 } [/latex] = 6 (1)
Solution 8.
Given : a5 + a9 = 30
a25 = 3a8
Now, a + 4d + a+8d = 30
⇒ 2a+ 12d = 30
⇒ a + 6d = 15 …(i) (1/2)
and, a + 24d=3a + 21d ⇒2a-3d = 0 …(ii) (1/2)
From eqs. (i) and (ii)

Now, put d = 2 in eq. (i)
a+ 12=15 ⇒ a = 3
Required A.P. = 3,5,7,………….. (1/2)
Solution 9.
Let the number of blue balls = x
∴ Total number ofballs = 5 + x
P (blue ball) = [latex s=2]\frac { x }{ 5+x } [/latex] (1/2)
P (red ball) = [latex s=2]\frac { 5 }{ 5+x } [/latex] (1/2)
Given that P (blue) = 2 × p (red)
[latex s=2]\frac { x }{ 5+x } [/latex] = 2 × [latex s=2]\frac { 5 }{ 5+x } [/latex]
⇒ [latex s=2]\frac { x }{ 5+x } [/latex] = [latex s=2]\frac { 10 }{ 5+x } [/latex]
On solving we get x = 10 (1)
Solution 10.
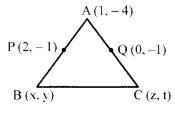
P is the mid-point ofAB
∴ x+1=4⇒x = 3 [By Mid-Point formula]
y-4 = -2 ⇒ y = 2
⇒ B(3,2) (1/2)
Similarly,
z + 1 = 0 ⇒z = -1
and t – 4 = -2 ⇒t = 2
⇒ C(—1,2)
∴ Area ∆ABC (1/2)
= [latex s=2]\frac { 1 }{ 2 } [/latex][1(2 – 2)+3(2+4)-1(-4-2)] ⇒[latex s=2]\frac { 1 }{ 2 } [/latex] ×24 = 12 sq units (1)
Solution 11.
Since, (3, a) lies on the line 2x – 3y = 5
So, 2 × 3 – 3a = 5 (1)
⇒ 6 —3a = 5 ⇒ a= [latex s=2]\frac { 1 }{ 3 } [/latex] (1)
Solution 12.
Total number of possible outcomes when two dice are thrown simultaneously =36 (1/2)
Sum of the numbers appearing on the dice
is a prime number i.e., 2,3,5,7 and 11
So, the possible outcomes are (1,1), (1,2), (2, 1), (1,4), (2,3), (3,2), (4,1), (1,6), (2,5),
(3,4), (4,3), (5,2), (6,1), (5,6) and (6,5).
Number of possible outcomes = 15 (1)
∴ Required probability = [latex s=2]\frac { 15 }{ 36 } [/latex] = [latex s=2]\frac { 5 }{ 12 } [/latex] (1/2)
Section-C
Solution 13.
Given integers are 81 and 237 such that 81 < 237.
Applying Euclid’s division lemma to 81 and 237, we get
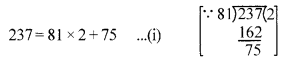
Since the remainder 75 ≠ 0. So, consider the divisor 81 and the remainder 75 and apply division lemma to get

The remainder at this stage is zero. So, the last divisor i.e. 3 is the HCF of 81 and 237.
To represent the HCF as a linear combination of the given two numbers, we start from the last but one step and successively eliminate the previous remainders as follows :
From (iii), we have
3 = 75 – 6 × 12
⇒3 = 75-(81 – 75 × 1) ×12
[Substituting 6 = 81 -75 × 1 obtained from (ii)]
⇒ 3 = 75 – 12 × 81 + 12 × 75
⇒ 3 = 13 × 75 – 12 × 81
⇒ 3 = 13 × (237-81 × 2)-12 × 81 [Substituting 75 = 237 – 81 × 2 obtained from (i)] (1)
⇒ 3 = 13 × 237 – 26 × 81 – 12 × 81
⇒ 3 = 13 × 237 – 26 × 81 – 12 × 81
⇒ 3 = 13 × 237-38 × 81
⇒ 3 = 237 × + 81 y, where x = 13 and
y = -38 ….v (1)
Solution 14.

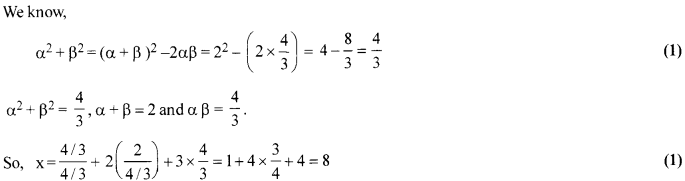
Solution 15.
Perimeter of shaded region
= Perimeter (QTR+ QAP + PSR) (1)
= π[latex]\left[ 5+\frac { 3 }{ 2 } \frac { 7 }{ 2 } \right] =\pi \left[ \frac { 20 }{ 2 } \right] [/latex] =10π = 31.4cm (2)
Solution 16.
Let the radius of spherical marble = 0.7 cm (1/2)
Volumeofl marble =[latex s=2]\frac { 4 }{ 3 } [/latex]πr3 = [latex s=2]\frac { 4 }{ 3 } [/latex]π(0.7)3 cm3 (1/2)
Volume of 150 marble = 200π(0.7)3 cm3 (1/2)
Let h be the rise in the height of water
∴ Volume of water raised = Volume of 150 marbles (1/2)
So, π × 72 × h = 200π(0.7)3 ⇒ h = [latex]\frac { 200\times 7\times 7\times 7 }{ 7\times 7\times 10\times 10\times 10 } [/latex]
⇒ h = 1.4 cm (1)
OR
Let the radius ofhemisphere = r
Now, volume ofhemisphere = [latex s=2]\frac { 2 }{ 3 } [/latex] πr3 (1/2)
Surface area ofhemisphere = 3πr2 (1/2)
A.T.Q, volume ofhemisphere = surface area ofhemisphere (1/2)
⇒ [latex s=2]\frac { 2 }{ 3 } [/latex] πr3 = 3πr2 ⇒r= [latex s=2]\frac { 9 }{ 2 } [/latex]units (1)
Solution 17.
Suppose the coordinates of vertex D are (x, y), then
Mid-point of AC = Mid-point of BD (For parallelogram ABCD) (1/2)

Solution 18.

OR

Solution 19.
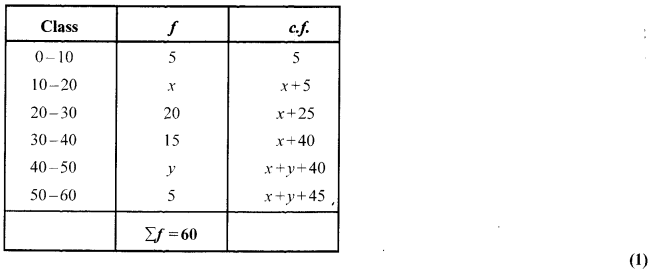

OR

Solution 20.
Let OP meet the circle at Q. Join AQ. As OP is equal to the diameter of the circle and OQ is the radius, so OQ = QP i.e. Q is the mid-point of OP. Since PA is tangent to the circle at A and OA is its radius, OA ⊥L AP i.e. ∠OAP = 90°.
In right triangle OAP, Q is mid-point of hypotenuse,
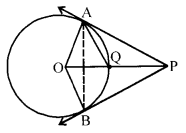
∴AQ = OQ = QP
Also OA = OQ (radii of same circle)
⇒ OA=OQ = AQ ⇒ ∆OAQ is equilateral
⇒ ∠AOQ = 60° ⇒ ∠AOP = 60°. (1)
In ∆OAP, ∠OPA + ∠AOP + ∠OAP =180°
⇒ ∠OPA+60°+ 90° = 180°
⇒ ∠OPA= 30°
⇒ ∠APB = 60° (∴OP is bisector of ZAPB) (1)
Also PA = PB ⇒ ∠PAB = ∠PBA.
In ∆PAB, ∠PAB + ∠PBA+ ∠APB = 180°
⇒ 2 ∠PAB+ 60° =180°
⇒ ∠PAB=60°
⇒ Triangle ABP is equilateral. (1)
Solution 21.
∴Letx2 = u, y2 = v
⇒ 2u + 3v=35 and [latex]\frac { u }{ 2 } +\frac { v }{ 3 } [/latex] = 5 (1/2)
⇒ 2u + 3v = 35 …(i)
⇒ 3u + 2v = 30 …(ii) (1/2)
Multiply (i) by 3 and (ii) by 2 and subtracting (ii) from (i), we have
⇒ 6u – 6u + 9v – 4v= 105 – 60
⇒ 5v = 45 ⇒v = 9
Substituting v = 9 in (1), we get 2u + 2 7 = 3 5
2u = 8 => u = 4 ⇒x2 = 4, y2 = 9
∴ x = ± 2,y = ± 3 is the required solution. (1)
Solution 22.

OR

Solution 23.
Suppose AB be a tower and there are two points C and D at the distances of 4 m and 16 m from the foot of the tower respectively

Since, the angles of elevation from C and D of the top of the tower are complementary.
So,e,+e2 = 90° …(i) (1/2)
Let the height of the tower be h.
Then, from equation (i), tan (θ1 + θ2) = tan 90° (1/2)
⇒ [latex]\frac { \tan { { \theta }_{ 1 } } +\tan { { \theta }_{ 2 } } }{ 1-\tan { { \theta }_{ 1 } } \tan { { \theta }_{ 2 } } } =\frac { 1 }{ 0 } [/latex]
⇒ 1- tan θ1 tan θ2 =0 ⇒ tan θ1 tan θ2 = 1 (1)
⇒ [latex]\frac { h }{ 4 } \times \frac { h }{ 16 } [/latex] = 1 ⇒ h<2 = 64 ⇒ h = 8 m (∵Height cannot be negative) (1)
Hence, the height of the tower is 8 m.
OR

Solution 24.

Solution 25.


OR
![]()

Solution 26.

Solution 27.

(i) Draw a line segment 4 cm.
(ii) Take a point P outside the circle and draw a secant PAB, intersecting the circle at A and B.
(iii) Produce AP to C such that AP = CP.
(iv) Draw a semi-circle with CB as diameter.
(v) Draw PD⊥L CB, intersecting the semi-circle at D.
(vi) With P as center and PD as radius draw arcs to intersect the given circle at T and T’.
(vii) Join PTand PT’. Then, PTand PT’ are the required tangents.
Solution 28.
First, convert the given frequency distribution table to a More Than Type frequency distribution table.

Now mark the lower limits along X-axis and cumulative frequencies along F-axis, and plot the points (400,230), (450,210), (500,175), (550,135), (600,103), (650,79), (700,52), (750,34). Join the points listed above by smooth freehand curve to obtain the more than type ogive.

Solution 29.
The equation (1 + m2) x2 + 2mcx + c2 – a2 = 0
For coincident (Repeated roots) D = 0 (1/2)
⇒ (2mc)2 -4(1+ m2) (c2 – a2) = 0 (1/2)
⇒ 4m2c2 – 4(c2 – a2 + m2c2 – m2a2) = 0 (1/2)
⇒ m2c2 – c2 + a2 – m2c2 + m2a2 = 0 (1/2)
⇒ m2a2 – c2 + a2 = 0 (1/2)
⇒ m2a2 + a2 = c2 ⇒ a2 (1 +m2) = c2 (1)
⇒ c = ±a[latex]\sqrt { 1+{ m }^{ 2 } } [/latex] Hence proved. (1/2)
OR
Put x = 4, we get 3(4)2 – 2m (4) + 2n = 0 (1/2)
⇒ 48-8m + 2n = 0 =>2n-8m = -48 ⇒ n-4m = -24 ….(i) (1)
Put x = -5, we get 3 (-5)2 – 2m (-5) + 2n = 0 (1/2)
⇒ 75 + 10m + 2n = 0 ⇒2n + 10m=-75 ….(ii) (1)
Solving (i) and (ii) we get, m = – [latex s=2]\frac { 3 }{ 2 } [/latex]and n = -30 (1)
Solution 30.
Let (a-3d),(a-d),(a + d),(a + 3d) are the four numbers
∴ Sum = 50
⇒ (a-3d) + (a-d) + (a + d) + (a-3d) = 50
⇒ a= [latex s=2]\frac { 25 }{ 2 } [/latex] (1)
also, (a + 3d) = 4(a-3d) (1)
⇒ 5 d=a
⇒ d = [latex s=2]\frac {5 }{ 2 } [/latex] (1/2)
5,10, 15 and 20 are the required numbers ofA.P. (1)
Download PDF file Click Here!!!
I hope you like the information and notes given by us. This will help you a lot in your upcoming exams. Here we are giving sample papers to all of you CBSE board students, through which all of you can score very well in your exams. In this post, we are giving you a sample paper of class 10 maths. hope you benefit from it. You can download the pdf file of this sample paper. cbse sample paper 2021 class 10 and cbse sample paper 2021 class 12
