Here we are giving sample papers to all of you CBSE board students, through which all of you can score very well in your exams. In this post, we are giving you a sample paper of class 10 maths. hope you benefit from it. You can download the pdf file of this sample paper.
CBSE Sample Papers for Class 10th Mathematics Paper 02 | CBSE Exam
| Board | CBSE |
| Class | X ( 10th ) |
| Subject | Mathematics |
| Sample Paper No. | Paper 02 |
| Category | CBSE Sample Papers |
Students who are going to appear for CBSE Class 10 Examinations are advised to practice the CBSE sample papers given here which is designed as per the latest Syllabus and marking scheme, as prescribed by the CBSE, is given here. Paper 1 of Solved CBSE Sample Paper for Class 10 Maths is given below with free pdf download solutions.
Time allowed: 3 Hours
Maximum Marks: 80
- All questions are compulsory.
- The question paper consists of 30 questions divided into four sections A, B, C, and D.
- Section A contains 6 questions of 1 mark each. Section B contains 6 questions of 2 marks each. Section C contains 10 questions of 3 marks each. Section D contains 8 questions of 4 marks each,
- There is no overall choice. However, an internal choice has been provided in four questions of 3 marks each and three questions of 4 marks each. You have to attempt only one of the alternatives in all such questions.
- Use of calculators is not permitted.
Question 1.
Identify: [latex s=2]\sqrt { \frac { 9 }{ \pi } } [/latex] as rational or irrational.
Question 2.
Find an arithmetic mean between 10[latex s=2]\frac { 1 }{ 2} [/latex] and 25[latex s=2]\frac { 1 }{ 2 } [/latex].
Question 3.
ABCD is a rectangle whose three vertices are B (4, 0), C (4, 3), and D (0, 3). What is the length of one of its diagonals?
Question 4.
If cos 2A = sin(A – 15°), find A.
Question 5.
If x = – [latex s=2]\frac { 1 }{ 2} [/latex], is a solution of the quadratic equation 3x2 + 2kx – 3 = 0, find the value of k.
Question 6.
In the figure of ∆ABC, the points D and E are on the sides CA, CB respectively such that DE || AB, AD = 2x, DC=x + 3,BE = 2x-1 and CE=x. Then, find x.

Question 7.
Find the HCF of 1,656 and 4,025 by Euclid’s division algorithm.
Question 8.
If the point P (k – 1,2) is equidistant from the points A (3,k) and B (k, 5), find the values of k.
Question 9.
The probability of selecting a rotten apple randomly from a heap of900 apples is 0.18. What is the number of rotten apples in the heap?
Question 10.
The probability of selecting a red ball at random from ajar that contains only red, blue, and orange balls
is [latex s=2]\frac { 1 }{ 4} [/latex]. The probability of selecting a blue ball at random from the same jar is [latex s=2]\frac { 1 }{ 3} [/latex]. If the jar contains 10 orange balls, find the total number of balls in the jar.
Question 11.
Sum of the ages of a father and the son is 40 years. If the father’s age is three times that of his son, then find their respective ages.
Question 12.
If the ratio of the sum of first n terms of two A.P’s is (7n + 1): (4n + 27), find the ratio of their wth terms.
Question 13.
Show that [latex s=2]\frac { 2 }{ 5\sqrt { 3 } } [/latex] is irrational
Question 14.
Obtain all other zeroes of the polynomial 4x4 + x3 – 72x2 – 18x, if two of its zeroes are 3[latex]\sqrt { 2 } [/latex] and -3[latex]\sqrt { 2 } [/latex] .
Question 15.
x-coordinate of a point P is twice its y-coordinate. If P is equidistant from Q (2, -5) and R (-3, 6), find the coordinates of P.
OR
The area of a triangle is 5 sq units. Two of its vertices are (2,1) and (3, -2). Ifthe third vertex is [latex s=2]\left( \frac { 7 }{ 2 } ,y \right) [/latex], find the value of y.
Question 16.
If [latex s=2]\frac { \cos { \alpha } }{ \cos { \beta } } [/latex] = m and [latex s=2]\frac { \cos { \alpha } }{ \sin { \beta } } [/latex] = n show that (m2 + n2)cos2 β n2
OR
Find the value of ‘x’ such that
2cos ec230° + x sin2 60°- [latex s=2]\frac { 3 }{ 4} [/latex]tan2 30° = 10
Question 17.
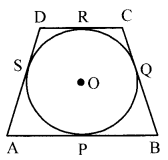
In the figure, a quadrilateral ABCD is drawn to circumscribe a circle, with centre O, in such a way that the sides AB, BC, CD, and DA touch the circle at the points P, Q, R, and S respectively. Prove that AB + CD = BC + DA.
Question 18.
In the given figure, ABCD is a rectangle of dimensions 21 cm × 14 cm. A semicircle is drawn with BC as diameter. Find the area and the perimeter of the shaded region in the figure.

Question 19.
A cubical block of side 10 cm is surmounted by a hemisphere. What is the largest diameter that the hemisphere can have? Find the cost of painting the total surface area of the solid so formed, at the rate of? 5 per 100 sq. cm [Use π=3.14].
OR
504 cones, each of diameter 3.5 cm and height 3 cm, are melted and recast into a metallic sphere. Find the diameter of the sphere and hence find its surface area. [Use π = [latex s=2]\frac { 22 }{ 7 } [/latex]]
Question 20.
Find the sum of values of a and b for which the following system of linear equations has infinite number of solutions:
2x + 3y = 7
(a+b+ 1)x + (a+2b + 2)y = 4(a+ b)+ 1
Question 21.
In the given figure, S and T trisect the side QR of a right triangle PQR. Prove that HPT2 = 3 PR2 + 5 PS2

OR
In the given figure PA, QB and RC, each are perpendicular to AC. Prove that [latex s=2]\frac { 1 }{ x } +\frac { 1 }{ z } =\frac { 1 }{ y } [/latex]

Question 22.
The mean and median of 100 observations are 50 and 52 respectively. The value of the largest observation is 100. It was later found that it is 110, not 100. Find the true mean and median.
Question 23.
If cos θ + [latex]\sqrt { 3 } [/latex] sin θ = 2sin θ
Show that sin θ – [latex]\sqrt { 3 } [/latex] cos θ = 2cos θ.
Question 24.
A well of diameter 4 m is dug 21 m deep. The earth taken out of it has been spread evenly all around it in the shape of a circular ring of width 3 m to form an embankment. Find the height of the embankment.
Question 25.
Solve the following for x :[latex s=2]\frac { 1 }{ 2a+b+2x } =\frac { 1 }{ 2a } +\frac { 1 }{ b } +\frac { 1 }{ 2x } [/latex]
OR
Solve for x: [latex s=2]\frac { 1 }{ x+1 } +\frac { 1 }{ x+2 } =\frac { 4 }{ x+4 } [/latex], x ≠ -1,-2,-4
Question 26.
Prove that the ratio of the areas of two similar triangles is equal to the ratio of the square of their corresponding sides
OR
In a right triangle, prove that the square of the hypotenuse is equal to the sum of the squares of the other two sides.
Question 27.
The angles of depression of the top and bottom of a 50 m high building from the top of a tower are 45° and 60° respectively. Find the height of the tower and the horizontal distance between the tower and the
building, (use [latex]\sqrt { 3 } [/latex] = 1.73)
OR
the vertical tower stands on a horizontal plane and is surmounted by a vertical flagstaff of height h. At a point on the plane, the angles of elevation of the bottom and the top of the flagstaff are α and β respectively. Prove that the height of the tower is ([latex s=2]\frac { h\tan { \alpha } }{ \tan { \beta } -\tan { \alpha } } \quad [/latex])
Question 28.
If [latex s=2]\frac { b+c-a }{ a } ,\frac { c+a-b }{ b } ,\frac { a+b-c }{ c } \quad [/latex] are in A.P. then prove [latex s=2]\frac { 1 }{ a } ,\frac { 1 }{ b } ,\frac { 1 }{ c } \quad [/latex] in A.P.
Question 29.
Draw a triangle ABC with side BC = 7 cm. ∠B = 45°, ∠A = 105°. Construct a triangle whose sides are (4/3) times the corresponding side of ∆ ABC.
Question 30.
On the annual day of school, age-wise participation of students is given in the following frequency distribution table:

Solutions:
Section-A
Solution 1.
[latexs=2]\sqrt { \frac { 9 }{ \pi } } =(3)\left( \frac { 1 }{ \sqrt { \pi } } \right) [/latex] = (rational) (irrational) = irrational (1)
Solution 2.

Solution 3.

According to the figure BD is the diagonal of ABCD. By distance formula BD
BD = [latex]\sqrt { { ({ x }_{ 2 }-{ x }_{ 1 }) }^{ 2 }+{ ({ y }_{ 2 }-{ y }_{ 1 }) }^{ 2 } } =\sqrt { { (4-0) }^{ 2 }+(0-3)^{ 2 } } [/latex]
= [latex]\sqrt { 25 } [/latex] = 5 units (1)
Solution 4.
sin(90° – 2A) = sin(A-15°)
⇒ 90°-2A = +4-15° ⇒ 3A = 105° (1/2)
∴ A = 35° (1/2)
Solution 5.
x = -[latex s=2]\frac { 1 }{ 2 } [/latex] is a solution of 3x2 + 2kx -3=0
Now, [latexs=2]{ 3\left( \frac { -1 }{ 2 } \right) }^{ 2 }+2k\left( \frac { -1 }{ 2 } \right) -3[/latex] = 0 (1/2)
[latex s=2]\frac { 3 }{ 4 } [/latex] -k -3 =0 ⇒ k = [latex s=2]\frac { -9 }{ 4 } [/latex] (1/2)
Solution 6.
[latex s=2]\frac { CD }{ AD } =\frac { CE }{ BE } [/latex] ⇒ [latexs=2]\frac { x+3 }{ 2x } =\frac { x }{ 2x-1 } [/latex] (1/2)
⇒ 5x = 3 ⇒ x = [latex s=2]\frac { 3 }{ 5 } [/latex] (1/2)
Section-B
Solution 7.
Since 4025 > 1656,
∴4025 =1656 × 2 + 713
1656 = 713 × 2 + 230
713 = 230 × 3+23 (1)
230 = 23 × 10+0
So, HCF (1,656,4,025) = 23 (1)
Solution 8.

Solution 9.
Since the number of apples in the given heap = 900
And the probability of selecting a rotten apple randomly = 0.18

Hence, the number of rotten apples in the heap will be 900 × 0.18 i.e.,162 (1)
Solution 10.
∵P (Red) = [latex s=2]\frac { 1 }{ 4 } [/latex], and, P (Blue) = [latex s=2]\frac { 1 }{ 3 } [/latex]
So, P (Orange) = 1-[latex]\frac { 1 }{ 4 } -\frac { 1 }{ 3 } =\frac { 5 }{ 12 } [/latex] (1)
Therefore, [latex s=2]\frac { 5 }{ 12 } [/latex] ×(Total no. of balls) = 10
Hence, total no. of balls = [latex s=2]\frac { 10\times 12 }{ 5 } [/latex] = 24 (1)
Solution 11.
Let ages of father and son be x and y respectively.
x+y = 40 …(i)
x = 3y ….(ii) (1)
By solving eqs. (i) and (ii)
x =30 andy = 10
Ages are 30 years and 10 years. (1)
Solution 12.
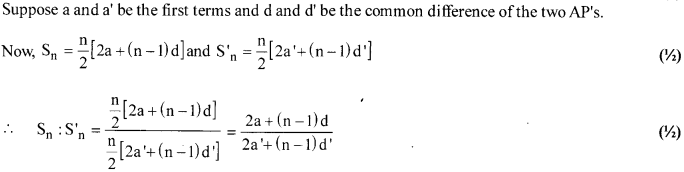

Section-C
Solution 13.
Let us assume [latex s=2]\frac { 2 }{ 5\sqrt { 3 } } [/latex], to the contrary, that [latex s=2]\frac { 2 }{ 5\sqrt { 3 } } [/latex] is rational.
∴ [latex s=2]\frac { 2 }{ 5\sqrt { 3 } } [/latex] = [latex s=2]\frac { p }{ q } [/latex] where p, q (q ≠ 0) are integers and p, q are co-prime. (1)
⇒ [latex s=2]\frac { 2q }{ 5p } [/latex] = [latex]\sqrt { 3 } [/latex] (1/2)
Since, 2, 5, p, q are integers
∴ [latex s=2]\frac { 2q }{ 5p } [/latex] is rational, and so [latex]\sqrt { 3 } [/latex] is rational. (1)
But this contradicts the fact that [latex]\sqrt { 3 } [/latex] is irrational
Hence, [latex s=2]\frac { 2 }{ 5\sqrt { 3 } } [/latex] is irrational. (1/2)
Solution 14.


Solution 15.
Let the y-coordinate of the point P be a.
And, its x-coordinate will be 2a.
So, the coordinates of the point P are (2a, a).
Since, the point P (2a, a) is equidistant from Q (2, -5) and R(-3,6).
∴ [latex]\sqrt { { (2a-2) }^{ 2 }+{ (a-(-5)) }^{ 2 } } =\sqrt { { (2a-(-3)) }^{ 2 }+{ (a-6) }^{ 2 } } [/latex] (1)
[latex]\sqrt { { (2a-2) }^{ 2 }+{ (a+5) }^{ 2 } } =\sqrt { { (2a+3) }^{ 2 }+{ (a-6) }^{ 2 } } [/latex]
So, [latex]\sqrt { { 5a }^{ 2 }+2a+29 } =\sqrt { { 5a }^{ 2 }+45 } [/latex] (1)
After squaring both sides, we get
5a2 + 2a + 29 = 5a2 + 45
5a2 + 2a – 5a2 = 45 – 29
Thus, a = 8
Hence, the coordinates of the point P are (16, 8).
OR

Solution 16.


OR

Solution 17.
As, the tangents drawn from the exterior point to a circle are equal in length. (1/2)
So, DR=DS ….(i)
AP= AS …(ii)
BP = BQ …(iii)
CR=CQ ….(iv) (1)

Adding(i), (ii), (iii) and (iv), we get
DR + AP + BP + CR = DS + AS + BQ + CQ (1/2)
⇒ (DR + CR) + (AP + BP) = (DS + AS) + (BQ + CQ)
⇒ CD + AB = DA + BC
⇒ AB+CD = BC + DA (Hence Proved). (1)
Solution 18.
Area of the shaded region
= Area of the rectangle – Area of the semi-circle (1/2)
(14×21) – [latex s=2]\frac { 1 }{ 2 } \times \frac { 22 }{ 7 } \times { 7 }^{ 2 }[/latex] (1/2)
= 294 – 77 = 217 cm2 (1/2)
Perimeter of shaded region = (2 × 21) +14 + [latex s=2]\left( \frac { 22 }{ 7 } \times { 7 } \right) [/latex] (1)
= 42+14 + 22 = 78 cm (1/2)
Solution 19.
∵ Largest possible diameter ofhemisphere = 10 cm
So, radius ofhemisphere = 5 cm (1/2)
Now, total surface area = 5(10)2 + 3.14 × (5)2 × 2 (1)
= 657 cm2 (1/2)
Hence, cost of painting = [latex s=2]\frac { 657\times 5 }{ 100 } [/latex] = ₹ 32.85
OR

Solution 20.


Solution 21.
S and T trisect the side QR.
Let QS = ST = TR = x units
Let PQ = y units (1/2)
In right ∆PQS, PS2 = PQ2 + QS2 (By Pythagoras Theorem)
= y2 + x2 …(i) (1/2)
In right ∆PQR, PT2 = (By Pythagoras Theorem)
= y2 + (2x)2 = y2 + 4x2 ….(ii) (1/2)
In right ∆PQR, PR22 = PQ2 + QR2(By Pythagoras Theorem)
=y2 + (3x)2 = y2 + 9x2 …(iii) (1/2)
R.H.S. = 3 PR2 + 5 PS2
= 3(y2 + 9x2)+ 5(y2+x2) [From (i) and (iii)]
= 3y2 + 27x2 + 5y2 + 5x2 = 8y2 + 32x2
= 8(y2 + 4x2) = 8PT2 = L.H.S. [From(ii)] (1)
Thus 8PT2 = 3PR2 + 5PS22
OR
In APAC and AQBC, We have
∠PAC = ∠QBC [Each = 90°]
∠PCA = ∠QCB [Common] (1)
∴∆PAC ~ ∆QBC
∴ [latex s=2]\frac { x }{ y } =\frac { AC }{ BC } [/latex] i.e. [latexs=2]\frac { y }{ x } =\frac { BC }{ AC } [/latex] ..(i) (1/2)

Solution 22.

Section-D
Solution 23.
(cos θ + [latex]\sqrt { 3 } [/latex] sin θ)2 + (sin θ – [latex]\sqrt { 3 } [/latex] cos θ)2
= cos2 θ + 3sin2 θ + 2 [latex]\sqrt { 3 } [/latex] cos θ sin θ + sin2 θ + 3cos2 θ – 2 [latex]\sqrt { 3 } [/latex] cos θ sin θ (1)
⇒ (2sin θ)2 + (sin θ – [latex]\sqrt { 3 } [/latex] cos θ)2 = (cos2 θ + sin2 θ) + 3 (sin2 θ + cos2 θ) (1)
⇒ (sin θ – [latex]\sqrt { 3 } [/latex] cos θ)2 = 4 – 4 sin2 θ (1/2)
⇒ (sin θ- [latex]\sqrt { 3 } [/latex] cos θ)2 = 4 cos2 θ (1)
⇒ sin θ – [latex]\sqrt { 3 } [/latex] cos θ = 2 cos θ (Hence proved) (1/2)
Solution 24.
Let r and h be the radius and depth of the well, respectively.
Here, r = [latex s=2]\frac { 4 }{ 2 } [/latex] = 2 m and h = 21 m (1/2)
Let R and H be the outer radius and height of the embankment, respectively.
So, R = r + 3= 2 + 3 = 5m (1)
As, volume of the earth to form the embankment = Volume of the earth dug out
π(R2-r2)H = πr2h (1)
∴ H = [latex s=2]\frac { { r }^{ 2 }h }{ { R }^{ 2 }-{ r }^{ 2 } } [/latex] (1/2)
∴ H = [latex s=2]\frac { { 2 }^{ 2 }\times 21 }{ { 5 }^{ 2 }-{ 2 }^{ 2 } } [/latex] = 4 m (1)
Solution 25.
Since, [latex s=2]\frac { 1 }{ 2a+b+2x } =\frac { 1 }{ 2a } +\frac { 1 }{ b } +\frac { 1 }{ 2x } [/latex]
[latex s=2]\frac { 1 }{ 2a+b+2x } =\frac { 2xb+4ax+2ab }{ (2a)(b)(2x) } [/latex] (1)
4abx = (2xb + 4ax + 2ab) (2a + b + 2x)
4abx = 12axb + 8a2x + 4a2b + 2xb2 + 2ab2 + 4x2b + 8ax2
x2 (4b + 8a) + x(8ab + 8a2 + 2b2) + (2ab2 + 4a2b) = 0 (1)
4x2 (2a + b) + x [4a (2a + b) + 2b (2a+ b)] + 2ab (b + 2a) = 0
4(2a + b) x[x + a] + 2b (2a + b) [x + a] = 0 (1)
(x + a) (2x + b) = 0 [ ∵ 2a + b ≠ 0]
x = -a, [latex s=2]\frac { -b }{ 2 } [/latex]
Hence, the value of x is -a and [latex s=2]\frac { -b }{ 2 } [/latex]. (1)
OR

Solution 26.

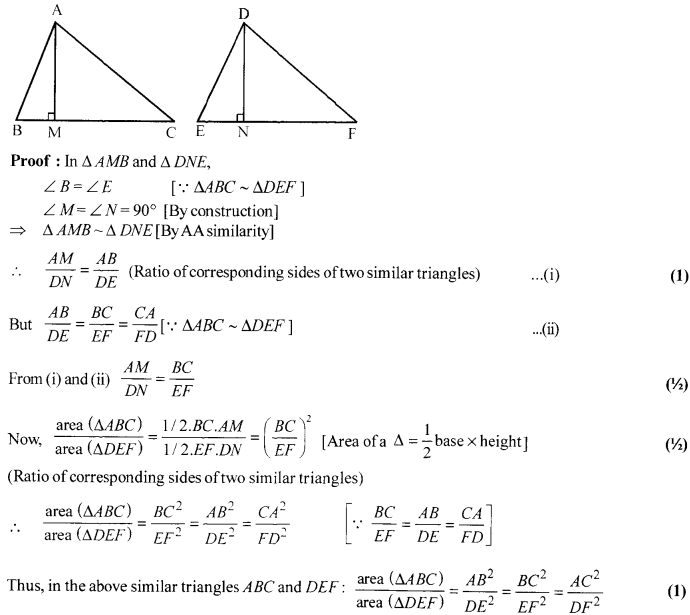
OR


Solution 27.

OR
![]()

Solution 28.

Solution 29.
Steps of construction:
1.DrawBC = 7cm.
2. Draw a ray BX and CY such that ∠CBX = 45° and ∠BCY =180°- (45° + 105°) = 30°
Suppose BX and CY intersect each other at A. ∆ ABC so obtained is the given triangle.
3. Draw a ray BZ making a suitable acute angle with BC on the opposite side of vertex A with respect to B BC.
4. Draw four (greater of 4 and 3 in 4/3) arcs intersecting the ray BZ at B1, B2, B3, B4 such that BB1 = B1B2 = B2B3 = B3B4.
5. Join B3 to C and draw a line through B4 parallel to B3C, intersecting the extended line segment BC at C’.
6. Draw a line through C’ parallel to CA intersecting the extended line segment BA at A’. Triangle A’BC’ so obtained is the required triangle. (1)

Solution 30.

Download PDF file Click Here!!!
I hope you like the information and notes given by us. This will help you a lot in your upcoming exams. Here we are giving sample papers to all of you CBSE Sample Paper board students, through which all of you can score very well in your exams. In this post, we are giving you a sample paper of class 10 maths. hope you benefit from it. You can download the pdf file of this sample paper.
