Here we are giving sample papers to all of you CBSE board students, through which all of you can score very well in your exams. In this post, we are giving you a sample paper of class 10 maths. hope you benefit from it. You can download the pdf file of this sample paper.
CBSE Sample Papers for Class 10th Mathematics Paper 01 | CBSE Exam
| Board | CBSE |
| Class | X ( 10th ) |
| Subject | Mathematics |
| Sample Paper No. | Paper 01 |
| Category | CBSE Sample Papers |
Students who are going to appear for CBSE Class 10 Examinations are advised to practice the CBSE sample papers given here which is designed as per the latest Syllabus and marking scheme, as prescribed by the CBSE, is given here. Paper 1 of Solved CBSE Sample Paper for Class 10 Maths is given below with free pdf download solutions.
Time allowed: 3 Hours
Maximum Marks: 80
General Instructions
- All questions are compulsory.
- The question paper consists of 30 questions divided into four sections A, B, C, and D.
- Section A contains 6 questions of 1 mark each. Section B contains 6 questions of 2 marks each. Section C contains 10 questions of 3 marks each. Section D contains 8 questions of 4 marks each,
- There is no overall choice. However, an internal choice has been provided in four questions of 3 marks each and three questions of 4 marks each. You have to attempt only one of the alternatives in all such questions.
- Use of calculators is not permitted.
Section – A
Question 1.
Explain why 13233343563715 is a composite number?
Question 2.
Solve the following quadratic equation for x :
4x2-4a2x + (a4-b4) = 0.
Question 3.
If the ratio of the corresponding sides of two similar triangles is 5 : 6, then find the ratio of their areas.
Question 4.
If the sum of n terms of an A.P. is given by Sn = (3n2 + 2n), find its nth term.
Question 5.
In fig., the area of triangle ABC (in sq. units) is :

Question 6.
Show that: cosec2 θ – tan2(90° – θ) = sin2θ + sin(90° – θ)
Section – B
Question 7.
Prove that [latex]\sqrt { 5 } [/latex] is irrational.
Question 8.
If the seventh term of an AP is [latex s=2]\frac { 1 }{ 9 } [/latex] and its ninth term is [latex s=2]\frac { 1 }{ 7 } [/latex], find its 63rd term.
Question 9.
A card is drawn at random from a well-shuffled pack of 52 playing cards. Find the probability of getting neither a red card nor a queen.
Question 10.
Determine the values of m and n so that the following system of linear equations have infinite number of solutions :
(2m — l)x + 3y-5=0
3x + (n – l) y-2 = 0
Question 11.
If point A (0,2) is equidistant from the points B (3, p) and C (p, 5), find p. Also, find the length of AB.
Question 12.
Two different dice are tossed together. Find the probability that the product of the two numbers on the top of the dice is 6.
Section – C
Question 13.
Prove that [latex s=2]\frac { 1 }{ 3+\sqrt { 11 } } [/latex] is irrational.
Question 14.
If a and P are the zeroes of the polynomial x2 + 4x + 3, find the polynomial whose zeroes are 1+ [latex s=2]\frac { \beta }{ \alpha } [/latex] and 1+ [latex s=2]\frac { \alpha }{ \beta } [/latex].
Polynomial Roots Calculator is a set of methods aimed at finding values of x for which F(x)=0 Rational Roots
Question 15.
Find the coordinates of points which trisect the line segment joining (1, -2) and (- 3.4).
OR
Find the area of the triangle formed by the points A (5,2), B (4, 7), and C (7, -4).
Question 16.
In fig., a circle inscribed in triangle ABC touches its sides AB, BC, and AC at points D, E, and F respectively. If AB = 12 cm, BC = 8 cm and AC = 10 cm, then find the lengths of AD, BE and CF.

Question 17.
Prove that tan2 θ + cot2 θ + 2 = sec2 θ + cosec2 θ = sec2θ cosec2θ
OR
If [latex s=2]\frac { \cos { \theta } -\sin { \theta } }{ \cos { \theta } -\sin { \theta } } [/latex] = [latex s=2]\frac { 1-\sqrt { 3 } }{ 1+\sqrt { 3 } } [/latex] then find the value of 0.
Question 18.
Solve the system of equations : ax + by = 1, bx + ay = [latex s=2]\frac { 2ab }{ { a }^{ 2 }+{ b }^{ 2 } } [/latex] .
Question 19.
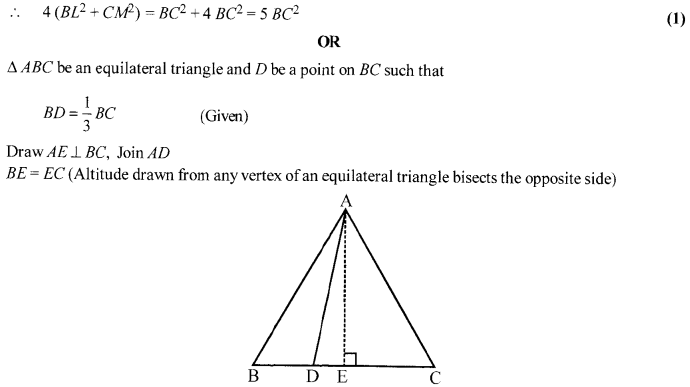
BL and CM are medians of ∆ ABC right angled at A. Prove that 4 (BL2 + CM2) = 5 BC2.
OR
In an equilateral triangle ABC, the side BC is trisected at D. Prove that 9 AD2 = 7 AB2.
Question 20.
In figure find the area of the shaded region [Use u = 3.14]
Question 21.
The data regarding marks obtained by 48 students of a class in a class test is given below. Calculate the modal marks of students.

Question 22.
How many silver coins, 1.75 cm in diameter and of thickness 2 mm, must be melted to form a cuboid of dimensions 5.5 cm × 10 cm × 3.5 cm?
OR
In the figure, from a cuboidal solid metallic block of dimensions 15 cm × 10 cm × 5 cm, a cylindrical hole of diameter 7 cm is drilled out. Find the surface area of the remaining block. [Use π = [latex s=2]\frac { 22 }{ 7 } [/latex] ]

Section – D
Question 23.
Solve for x : [latex s=2]\frac { 2x }{ x-3 } +\frac { 1 }{ 2x+3 } +\frac { 3x+9 }{ (x-3)(2x+3) } [/latex] = 0 , x ≠ 3, -[latex s=2]\frac { 3 }{ 2 } [/latex]
OR
Solve for x: [latex s=2]\frac { 1 }{ (x-1)(x-2) } +\frac { 1 }{ (x-2)(x-3) } =\frac { 2 }{ 3 } [/latex] ,x≠ 1,2,3
Question 24.
If sec θ + tan θ = p, show that sec θ – tan θ = [latex s=2]\frac { 1 }{ p } [/latex] . Hence, find the values of cos θ and sin θ.
Question 25.
A thief runs away from a police station with a uniform speed of 100 m/minute. After one minute, a policeman runs behind the thief to catch him. He goes at a speed of 100 m/minute in first minute and increases his speed by 10 m/min in each succeeding minute. How many minutes will the policeman take to catch the thief?
Question 26.
Construct a A ABC in which AB = 5 cm, BC = 6 cm and AC = 7 cm. Now, construct a triangle similar to AABC such that each of its sides is two-third of the corresponding sides of A ABC.
Question 27.
A solid wooden toy is in the form of a hemisphere surmounted by a cone of same radius. The radius of
hemisphere is 3.5 cm and the total wood used in the making of toy is [latex s=2]166\frac { 5 }{ 6 } [/latex] cm3. Find the height of the toy.
OR
Also, find the cost of painting the hemispherical part of the toy at the rate of ₹10 per cm2.[Use π = [latex s=2]\frac { 22 }{ 7 } [/latex] ]
Question 28.
Prove that if a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, then the other two sides are divided in the same ratio.
OR
If a line divides any two sides of a triangle in the same ratio, then prove that the line is parallel to the third side.
Question 29.
Two ships are there in the sea on either side of a lighthouse in such a way that the ships and the lighthouse are in the same straight line. The angles of depression of two ships as observed from the top of the lighthouse are 60°and 45°. If the height of the lighthouse is 200 m, find the distance between the two ships. [Use [latex s=2]\sqrt { 3 } [/latex] =1.73].
OR
The angle of elevation of an airplane from a point on the ground is 60°. After a flight of 30 seconds, the angle
of elevation becomes 30°. If the airplane is flying at a constant height of 3000 [latex s=2]\sqrt { 3 } [/latex] m, find the speed of the airplane.
Question 30.
Ifthe mean of the following data is 14.7, find the value ofp and q.

Solutions
Section – A
Solution 1.
Since the given number ends in 5. which means it is a multiple of 5. Hence it is a composite number. (1)
Solution 2.
(4x2 – 4a2 + a4) – b4 = 0 (1/2)
⇒ (2x – a2)2 – (b2)2 = 0
∴ (2x – a2 + b2) (2x – a2 – b2) = 0
(∵a2 – b2 = (a + b) (a – b))
⇒ x = [latex s=2]\frac { { a }^{ 2 }-{ b }^{ 2 } }{ 2 } [/latex] ,[latex s=2]\frac { { a }^{ 2 }+{ b }^{ 2 } }{ 2 } [/latex] (1/2)
Solution 3.
Suppose the triangles be ∆ABC and ∆DEF
[latex s=2]\frac { ar(\triangle ABC) }{ ar(\triangle DEF) } [/latex] = ([latex s=2]\frac {5 }{ 6 } [/latex])2 = [latex s=2]\frac {25 }{ 36 } [/latex] (1)
Hence, required ratio is 25 : 36
Solution 4.
It is given that Sn = 3n2 + 2n
∴Sn-1 = 3 (n-1)2 + 2(n- 1) = 3n2-4n + 1, nthterm, tn (1/2)
= (Sum ofnterms)-[Sumof(n-1)terms]
= Sn – Sn-1 = (3n2 + 2n) – (3n2 – 4n + 1) = (6n -1) (1/2)
Solution 5.
Since, the coordinates of given triangle are A(1, 3), B (-1,0) and C (4,0). So, the area of triangle ABC
= [latex s=2]\frac { 1 }{ 2 } [/latex][1(0-0)+(-1)(0-3)+(3-0)] (1/2)
= [latex s=2]\frac { 1 }{ 2 } [/latex] [3+12] = [latex s=2]\frac { 15 }{ 2 } [/latex] = 7.5.sp. unis. (1/2)
Solution 6.
LHS = cosec2θ – tan2(90° -θ)
= cosec2θ – cot2θ (∵ cot θ = tan(90° -0)) (1/2)
= 1 = sin2θ + cos2θ
= sin2θ + sin2(90° – θ) = RHS (1/2)
Section – B
Solution 7.
Let if possible [latex ]\sqrt { 5 } [/latex] = [latex s=2]\frac { p }{ q } [/latex], where p and q are co-prime.
∴5 × q2 = p2 ….(i)
⇒ 5 divides p
⇒ p = 5 × P1; p1 is an integer. ….(ii) (1/2)
From (i) and (ii),
5 × q2 = (5 ×p1)2 = 52 × p12
⇒ q2 = 5 × p12 ⇒ 5 divides q (1/2)
⇒ q = 5 × q1; q1 is an integer …..(iii) (1/2)
From (ii) and (iii), we find 5 a common factor of p and q. It contradicts that p and q are co-prime. Hence, [latex]\sqrt { 5 } [/latex] is an irrational number. (1/2)
Solution 8.

Solution 9.
Total number of events = 52 (1/2)
In a pack of 52 playing cards, there are 2 red queens and 2 black queens, respectively.
Number of cards that are neither red nor queen = 52 – (26 + 2) = 24 (1/2)
Now, favourable number of events = 24
So, required probability = [latex s=2]\frac { 24 }{ 52 } [/latex] = [latex s=2]\frac { 6 }{ 13 } [/latex] (1)
Solution 10.


Solution 11.

Solution 12.
P (Product = 6) = P [(1,6), (2,3), (3,2), (6,1)] (1)
Probability = [latex s=2]\frac { 4 }{ { 6 }^{ 2 } } [/latex] = [latex s=2]\frac { 4 }{ 36 } [/latex] = [latex s=2]\frac { 1 }{ 9 } [/latex] (1)
Hence, the probability that the product of the two numbers on the top of the dice is 6, will be [latex s=2]\frac { 1 }{ 9 } [/latex].
Section – C
Solution 13.

Solution 14.


Solution 15.

Solution 16.


Solution 17.
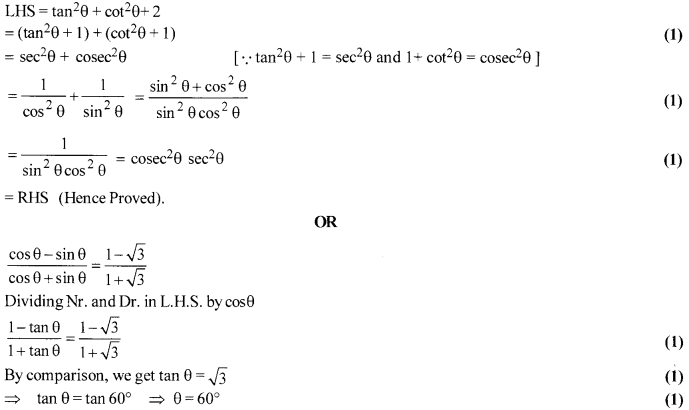
Solution 18.


Solution 19.


Solution 20.

Area of sq. ABCD = (side)2= 196 cm2 (1)
Area of small sq. = (side)2 = 42=16cm2
Area of 4 semi-circles = 4 × [latex s=2]\frac { 1 }{ 2 } [/latex]πr2 = [4.[latex s=2]\frac { 1 }{ 2 } [/latex](3.14)(2)2] = 25.12 cm2
∴ Area of shaded region = (196- 16-25.12)cm2= 154.88 cm2 (1)
Solution 21.

Solution 22.

Section – D
Solution 23.


Solution 24.


Solution 25.
![]()
Let the policeman catch the thief at a distance of x meters from the police station.
By the time the policeman starts, the thief is at a distance of 100 m.
So, by the time thief travels x -100 more distance with a speed of 100 m/min, the policeman travels x m to catch him, increasing speed by 10 m every minute. (1/2)
Time taken by the thief to come to the catch point from the time the policeman starts,
t = [latex s=2]\frac { x-100 }{ 100 } [/latex] ….(i) (1)
Distance traveled by the policeman in the first minute = 100 m, and in the second minute = 110, in third minute = 120.
and in tth minute = 100 +(t – 1) 10
Total distance covered by the policeman in t minutes is x [latex s=2]\frac { t }{ 2 } [/latex]{200+(t-1)10} (1)

Solution 26.
(i) Draw a line segment AB = 5 cm.

(ii) With A as center and radius = 7 cm, draw an arc above AB. (1)
(iii) With B as center and radius = 6 cm, draw another arc, intersecting the arc drawn in step (ii) at C.
(iv) Join AC and BC to obtain ∆ ABC.
(v) Below AB, draw a ray AX making a suitable acute angle with AB on opposite side ofC with respect to AB.
(vi) Draw three arcs intersecting the ray AX at A1, A2, A3 such that AA1 = A1A2 = A2A3.
(vii) Join A3B.
(viii) Draw A2B’ || A3B, meeting AB at B’.
(ix) From B’, draw B’C’ || BC, meeting AC at C’.
∆AB’C’ is the required triangle, each of whose sides is two-third of the corresponding sides of
∆ ABC.
Solution 27.


Solution 28.


OR

Solution 29.
Let AB is the height of lighthouse = 200m (1)
Two ships are at points C and D on either side of AB (light house)
In ∆ABC,
tan 60° =[latex s=2]\frac { AB }{ BC } [/latex] ⇒BC = [latex s=2]\frac { 200\sqrt { 3 } }{ 3 } \quad =\quad \frac { 200\times 1.73 }{ 3 } [/latex] = 115.33 m

In ∆ABD,
tan 45° = [latex s=2]\frac { AB }{ BD } [/latex] ⇒BD = 200 (1)
Distance between both ships = BC +BD
= 1115.33+200 = 315.33 cm (1)
OR

According to figure,
In ∆ABP, tan 60° =[latex s=2]\frac { AB }{ BP } [/latex] = [latex s=2]\frac { h }{ x } [/latex] = [latex s=2]\frac { 3000\sqrt { 3 } }{ x } [/latex] (1)
⇒ h = [latex s=2]\sqrt { 3 } [/latex]x ⇒ x= 3000m ….(i)
In APDC, tan 30° = [latex s=2]\frac { h }{ x+BD } [/latex] (1)
x + BD= h[latex s=2]\sqrt { 3 } [/latex] ….(ii)
From (i) and (ii)
x + BD=3x ⇒ BD = 2x
⇒ BD = 2(3000)
⇒ BD= 6000m (1)
Speed of aeroplane = [latex]\frac { BD }{ 30Sec } [/latex] = [latex]\frac { 6000 }{ 30 } [/latex] = 200 m/cm (1)
Solution 30.


Download PDF file Click Here!!!
Here we are giving sample papers to all of you CBSE board students, through which all of you can score very well in your exams. In this post, we are giving you a sample paper of class 10 maths. hope you benefit from it. You can download the pdf file of this sample paper.
