Here we are giving sample papers to all of you CBSE board students, through which all of you can score very well in your exams. In this post, we are giving you a sample paper of class 10 maths. hope you benefit from it. You can download the pdf file of this sample paper. cbse sample paper 2021 class 10 and cbse sample paper 2021 class 12
CBSE Sample Paper for Class 10th Mathematics Paper 07 | CBSE Exam | CBSE Notes
| Board | CBSE |
| Class | X ( 10th ) |
| Subject | Mathematics |
| Sample Paper No. | Paper 07 |
| Category | CBSE Sample Paper |
Students who are going to appear for CBSE Class 10 Examinations are advised to practice the CBSE sample papers given here which is designed as per the latest Syllabus and marking scheme, as prescribed by the CBSE, is given here. Paper 1 of Solved CBSE Sample Paper for Class 10 Maths is given below with free pdf download solutions.

Time allowed: 3 Hours
Maximum Marks: 80
General Instructions
- All questions are compulsory.
- The question paper consists of 30 questions divided into four sections A, B, C, and D.
- Section A contains 6 questions of 1 mark each. Section B contains 6 questions of 2 marks each. Section C contains 10 questions of 3 marks each. Section D contains 8 questions of 4 marks each,
- There is no overall choice. However, an internal choice has been provided in four questions of 3 marks each and three questions of 4 marks each. You have to attempt only one of the alternatives in all such questions.
- Use of calculators is not permitted.
Question 1.
What type of decimal expansion does a rational number have? How can you distinguish it from the decimal expansion of irrational numbers?
Question 2.
Coordinates of P and Q are (4,-3) and (-1, 7). What is the abscissa of a point R on the line segment PQ such that [latex]\frac { PR }{ PQ } [/latex] = [latex]\frac { 3 }{ 5 } [/latex] ? (NTSE 2012)
Question 3.
For what value of k will k + 9, 2k – 1 and 2k + 7 be the consecutive terms of an A.P.?
Question 4.
For the equation 3×2 + px + 3 = 0, if one of the roots is the square of the other then find p. (NTSE 2014-2015)
Question 5.
Find the value of sin (45° + θ) – cos (45° – θ)
Question 6.
In Fig., if PQ || RS, prove that ∆ POQ ~ ∆ SOR

(Section-B)
Question 7.
When 2256 is divided by 17 then find the remainder.
Question 8.
In what ratio, the line segment joining the points (3,5) & (-4,2) is divided by the y-axis?
Question 9.
Find the solution of the pair equations [latex s=2]\frac { x }{ 10 } [/latex] + [latex s=2]\frac { y }{ 5 } [/latex] – 1= 0 and [latex s=2]\frac { x }{ 8 } [/latex] + [latex s=2]\frac { y }{ 6 } [/latex] = 15. Hence, find λ, if y = λx + 5.
Question 10.
Find the sum of first 24 terms of the sequence whose nth term is an = 3+[latex s=2]\frac { 2n }{ 3 } [/latex]
Question 11.
A girl calculates that the probability of her winning the first prize in a lottery is 0.08. If6000 tickets are sold,
Question 12.
A book containing 100 pages is opened at random. Find the probability that a double page is found.
(Section-C)
Question 13.
Show that any positive odd integer is of form 8q ± 1 and 8q ± 3, where q is some integer.
Question 14.
If a and 8 are the zeroes of the quadratic polynomial f(x) = ax2 + bx + c then evaluate [latex]\frac { { \alpha }^{ 2 } }{ { \beta }^{ 2 } } +\frac { { \beta }^{ 2 } }{ { \alpha }^{ 2 } } [/latex]
Question 15.
In the given fig, BD ⊥ AC and CE ⊥ AB. Prove that
(i) ∆AEC ~ ∆ADB
(ii) [latex s=2]\frac { CA }{ AB } [/latex] = [latex s=2]\frac { CE }{ DB } [/latex]
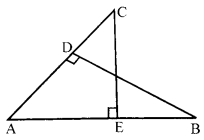
OR
In the given fig, [latex s=2]\frac { OA }{ OC } [/latex] = [latex s=2]\frac { OD }{ OB } [/latex] prove that ∠A = ∠C and ∠B = ∠D

Question 16.
Prove that the area of a triangle with vertices (t, t – 2), (t + 2, t + 2) and (t + 3, t) is independent of t.
OR
The three vertices of a parallelogram, taken in order, are (1, -2), (3,6) and (5,10). Find the coordinates of its fourth vertex.
Question 17.
In the given figure, PA and PB are tangents to the circle from an external point P. CD is another tangent touching the circle at Q. If PA = 12 cm, QC = QD = 3 cm, then find PC + PD.

Question 18.
Calculate the mean of the following frequency distribution :

Question 19.
In the figure, ABCD is a square of a side 10 cm and semicircles are drawn with each side of the square as diameter. Find the area of the shaded region.

Question 20.
A lending library has a fixed charge for the first three days and an additional charge for each day thereafter. Roohi paid ₹ 27 for a book kept for seven days, while Shushama paid₹ 21 for the book she kept for five days. What is the fixed charge?
Question 21.
Without using trigonometric tables, prove that:- tan7° tan 23° tan 60° tan 67° tan 83° = [latex]\sqrt { 3 } [/latex]
OR
If 5 tan θ = 4, then find the value of [latex s=2]\frac { 5\sin { \theta } -3\cos { \theta } }{ 5\sin { \theta } +2\cos { \theta } } [/latex]
Question 22.
A copper rod of diameter 1cm and length 8 cm, is drawn into a wire of length 18 m of uniform thickness. Find the thickness of the wire.
OR
If a solid piece of iron in the form of a cuboid of dimensions 49 cm × 33 cm × 24 cm, is moulded to form a solid sphere. Find the radius of the sphere
(Section-D)
Question 23.
In a right triangle, prove that the square of the hypotenuse is equal to the sum of the squares of the other two sides.
OR
In a triangle, if the square of one side is equal to the sum of the squares of the other two sides, then prove that the angle opposite to the first side is a right angle.
Question 24.
What is the value of x if
cot x = [latex s=2]\frac { 5 }{ 3 } [/latex] tan 130 tan 37° tan 45 ° tan 53° tan 77° -[latex s=2]\frac { 2 }{ 3 } [/latex] cosec2 58° + [latex s=2]\frac { 2 }{ 3 } [/latex] cot 58° tan 32°.
Question 25.
Solve the equation: [latex s=2]\left( \frac { 2x-3 }{ x-1 } \right) -4\left( \frac { x-1 }{ 2x-3 } \right) [/latex] = 3 x ≠ 1, 3/2
Question 26.
Find the median of the following data :

OR
The median of the following data is 525. Find the values of* and y if the total frequency is 100.

Question 27.
Find the volume and total surface area of a tumbler in the form of a frustum of a cone, if the diameter of the ends are 6.50 cm and 3.50 cm and the perpendicular height of the tumbler is 7.80 cm.
Question 28.
Draw a circle of radius 4 cm. Draw two tangents to the circle inclined at an angle of 60° to each other.
Question 29.
If the ratio of the sum of the first n terms oftwoA.Ps is (7n+ 1): (4n + 27), then find the ratio of their 9th terms.
Question 30.
An aeroplane is flying at a height of 300 m above the ground. Flying at this height, the angles of depression from the aeroplane of two points on both banks of a river in opposite directions are 45° and
60° respectively. Find the width of the river. [Use [latex]\sqrt { 3 } [/latex] = 1.732]
OR
The angle of elevation of a cloud from a point 60 m above the surface of the water of a lake is 30° and the angle of depression of its shadow in the water of the lake is 60°. Find the height of the cloud from the surface of the water.
Solutions
(Section-A)
Solution 1.
A rational number is either terminating or non-terminating repeating.
An irrational number is non-terminating and non-repeating. (1)
Solution 2.
P (4, -3) and Q (-1,7)
PR: RQ = 3:2
4 × 2 + (-1) × 3
Abscissa = [latex s=2]\frac { 4\times 2+(-1)\times 3 }{ 3+2 } [/latex]= 1 (1)
Solution 3.
Given k + 9,2k – 1 and 2k + 7 are in AP.
∴ 2(2k – 1) = (k + 9)+(2k + 7) [By Arithmetic mean] (1/2)
⇒ 4k-2 = 3k+16 ⇒ k=18 (1/2)
Solution 4.
α + α2 = [latex s=2]\frac { -p }{ 3 } [/latex] ………..(i)
α3 = [latex s=2]\frac { 3 }{ 3 } [/latex] = 1 =>(α- l)(α3+ α+ 1) = 0 ⇒ α = 1
∴ p= – 6 (∵From (i)) (1)
Solution 5.
Given that
sin (45° + θ) – cos (45° – θ) = cos [90° – (45° + θ)] – cos (45° – θ) [∵ cos (90° – θ) = sin θ]
= cos (45° – θ) – cos (45° – θ) = 0 (1)
Solution 6.
PQ || RS (Given)
So, ∠P = ∠S (Alternate angles)
and ∠Q=∠R (1/2)
Also, ∠POQ = ∠ SOR (Vertically opposite angles)
Therefore, ∆POQ ~ ∆SOR (AAA similarity criterion) (1/2)
Solution 7.

Solution 8.

Solution 9.

Solution 10.

Solution 11.
P (winning) = 0.08
Total tickets sold = 6000
Let the number of tickets she bought be x, then probability of winning =[latex s=2]\frac { x }{ 6000 } [/latex] (1)
⇒[latex s=2]\frac { x }{ 6000 } [/latex] = 0.08 ⇒ x = 6000 × 0.08 ⇒ x = 480 (1)
Thus the girl bought 480 tickets.
Solution 12.
S= {1,2,3, ,100} (1/2)
n(S)= 100
E ={ 11,22,33,44, 55,66,77, 88,99} (1)
n(E) = 9
∴P(E) = [latex s=2]\frac { 9 }{ 100 } [/latex] (1/2)
Solution 13.
Let a and b be two positive integers where a is odd.
Applying division lemma a = 8q + r where 0 < r < 8
So, r can take any of the values 0, 1,2,3,4,5,6,7
Therefore, a= 8q, 8q + 1, 8q + 2, 8q + 3, 8q + 4,
8q + 5, 8q + 6, 8q + 7 (1)
Since, a is odd.
Therefore, a cannot take values 8q, 8q + 2, 8q + 4, 8q + 6 since they can expressed as multiples of 2.
So, a will take values 8q+ 1,8q + 3, 8q + 5, 8q + 7. (1)
Also, 8q + 5 = 8q + 8 – 3 = 8 (q + 1) – 3 = 8q’ — 3
where q’ = q + 1, 8q + 7 = 8q + 8 – 1 =8q’- 1
So, every positive odd integer is of form 8q ± 1, 8q ± 3. (1)
Solution 14.

Solution 15.
Given: In the fig., BD ⊥ AC and CE ⊥AB
To prove: (i) ∆AEC ~ ∆ADB
(ii) [latex s=2]\frac { CA }{ AB } [/latex] = [latex s=2]\frac { CE }{ DB } [/latex] (1)

Proof (i) In ∆AEC and ∆ADB
∠1 = ∠2 (each 90°)
∠A = ∠A (common)
∴ ∆AEC ~ ∆ADB (by AArule)
(ii) ∆AEC ~ ∆ADB
[latex s=2]\frac { CA }{ AB } [/latex] = [latex s=2]\frac { CE }{ DB } [/latex] (∵ Angles are similar ∴ corresponding sides are proportional) (1)
Hence proved
OR
[latex s=2]\frac { OA }{ OC } [/latex] = [latex s=2]\frac { OD }{ OB } [/latex]

To prove: ∠A = ∠C and ∠B = ∠D (1)
Proof: In ∆AOD and ∆BOC
[latex s=2]\frac { OA }{ OC } [/latex] = [latex s=2]\frac { OD }{ OB } [/latex] (Given)
and ∠AOD = ∠BOC (Vertically opposite angles)
∴ ∆AOD ~ ∆BOC (by SAS) (1)
∴ ∠A = ∠C and ∠B = ∠D (C.P.C.T.) (1)
Solution 16.
Let A (t, t – 2), B (t + 2, t + 2) and C (t + 3, t) be the vertices of the given triangle. (1/2)
Since the area of the triangle having vertices (x1, y1), (x2, y2) and(x3, y3)

Therefore, the area of the triangle with specified vertices is independent of t. (1/2)
OR
Let the fourth vertex be D (a, b)
Let the diagonals AC and BD intersect at E,

We know that the diagonals of a parallelogram bisect each other.
∴ E is the mid-point of AC as well as that of BD.
mid-point of AC is

Hence, The fourth vertex of the given parallelogram is D (3,2). (1)
Solution 17.
Given: PA and PB are tangents to the circle from an external point P. CD is another tangent at Q. PA= 12 cm, QC = QD = 3 cm

To find: PC + PD (1/2)
Proof: PA = PC + AC
12 = PC+ 3
[∵ QC = AC = 3 cm, tangents from external point to a circle are equal in length]
PC = 9 cm …(i) (1)
Similarly, BD = QD = 3 cm
and PB = PA =12 cm (1/2)
PB = PD + BD
12 = PD +3
PD = 9 cm
Now, PC + PD = 9 + 9 = 18 cm (1)
Solution 18.

Solution 19.
We mark the area of unshaded regions as A1, A2, A3 and A4 as shown in the figure.
Area of the shaded region = Area of the square ABCD – Area of the unshaded portion (A1+A2+A3+ A4).

Area of unshaded region A1+A3= Area of square ABQD – Area of the semi-circle on BC as diameter- Area of the semi-circle on AD as diameter.

Similarly, area of unshaded region A2 – A4 = Area of square ABCD – Area of the semi-circles on diameter AB and DC
So, Area A2+A4 = 102 -2× [latex s=2]\frac { \pi \times { 5 }^{ 2 } }{ 2 } [/latex] =100-25π.
So,Area A1 + A2 + A3 + A4 = 200-50π.
Area of the shaded region = Area of square ABCD – Area (A1 + A2 + A3 + A4) (1)
= 102-(200-50π)
= (100-200 + 50 π)sq. cm.
= 50 π -100 = 50 (π – 2) sq. cm.
= 50 (3.14-2)= 50 × 1.14 = 57 cm2. (1)
Solution 20.
x = F ixed charge
y = Additional charge for each day
x + 4y = 27 …(i)
x + 2y = 21 …(ii) (1)
⇒ (x + 4y)-(x+ 2y) = 27-21 => 2y = 6 ⇒y = 3 (1)
∵ x + 2y=21 =>orx + 2(3) = 21 ⇒ x= ₹ 15 (1)
Solution 21.
L.H.S.
= tan 7° tan 23° tan 60° tan 67° tan 83°= tan 7° tan 83° tan 23° tan 67° tan 60° (1)
= tan 7° cot 7° tan 23° cot 23° tan 60°(1)

OR


Solution 22.
Volume of rod = πr2h = π × (1/2)2 × (8) = 2πcm3 ….(i) (1)
Length of wire of same volume = 18m = 1800 cm.
Let ‘r’ be the radius of cross-section of wire (1/2)
∴ Volume = πr2h
Volume of wire = πr2 × 1800 ….(ii)
From (i) & (ii), πr2 × 1800 = 2π
r2 = 2/1800 =>r2= 1/900 =>r=1/30cm. (1)
Thickness of wire = diameter of cross-section = 2r = 2 × [latex s=2]\frac { 1 }{ 30 } [/latex] = [latex s=2]\frac { 1 }{ 15 } [/latex] = 0.067 cm (approximately) (1/2)
OR
Given, dimensions of the cuboid
= 49 cm x 33 cm x 24 cm
Now, volume of the cuboid
= 49x33x24 = 38808 cm3
Let the radius of the sphere is r, then (1/2)
Volume of the sphere = [latex s=2]\frac { 4 }{ 3 } [/latex]πr3 (1/2)
According to the given condition
Volume of the sphere = Volume of the cuboid (1/2)

(Section-D)
Solution 23.
Given: A triangle ABC in which ZB = 90°.

To prove : ACsup>2 = ABsup>2 + BCsup>2 or (Hypotenuse)sup>2 = (Base)sup>2 + (Perpendicular)sup>2
Construction : From B, drawBD⊥ AC. (1)
Proof: Since BD ⊥AC.
∴∆ADB ~ ∆ABC
∴[latex s=2]\frac { AD }{ AB } [/latex] = [latex s=2]\frac { AB }{ AC } [/latex] ⇒AB2 =AC ×AD …(i) (1)

OR

Solution 24.

Solution 25.

Solution 26.

OR


Solution 27.



Solution 28.
Steps of construction:
1. Draw a circle of radius 4 cm, with O as the centre.
2. Take a point A on the circumference of the circle and join OA. Draw a perpendicular to OA at A.
3. Draw a radius OB, making an angle of 120° with OA.
4. Draw a perpendicular to OB at B. Suppose these perpendiculars intersect at P.

Here, PA and PB are two tangents drawn to the circle inclined at an angle of 60° to each other.
Justification
The construction can be justified by proving that
∠APB = 60°.
∠OAP = 90° (By Construction)
∠OBP = 90° (By Construction)
∠AOB=120° (By Construction)
The sum of all interior angles of a quadrilateral is 360°,.
∠OAP + ∠AOB + ∠OBP + ∠APB = 360° .
⇒ 90°+120°+ 90° +∠APB = 360° (1)
⇒ ∠APB = 60°
Solution 29.

Solution 30.

OR

Download PDF file Click Here!!!
I hope you like the information and notes given by us. This will help you a lot in your upcoming exams. Here we are giving sample papers to all of you CBSE board students, through which all of you can score very well in your exams. In this post, we are giving you a sample paper of class 10 maths. hope you benefit from it. You can download the pdf file of this sample paper.
